Random Real Number from [2,10]
Suppose you choose at random a real number X from the interval [2,10].
(a) Find the density function f(x) and the probability of an event E for this experiment, where E is a subinterval [a,b] of [2,10].
(b) From (a), find the probability that X > 5, that 5 < X < 7, and that X2 −12X+35>0.

Density Function f(x) = Cx
Suppose you choose a real number X from the interval [2,10] with a density
function of the form
f(x) = Cx ,
where C is a constant.
(a) Find C.
(b) Find P(E), where E = [a,b] is a subinterval of [2,10].
(c) Find P(X > 5), P(X <7), and P(X2 −12X +35> 0).

Density Function f(x) = C/x
Suppose f(x)=Cxf(x) = \frac{C}{x}f(x)=xC.
Same as Exercise above, but suppose
f(x) = Cx .

Density Function f(x) = C/x
Suppose you throw a dart at a circular target of radius 10 inches.
Assuming that you hit the target and that the coordinates of the outcomes are chosen
at random, find the probability that the dart falls
(a) within 2 inches of the center.
(b) within 2 inches of the rim.
(c) within the first quadrant of the target.
(d) within the first quadrant and within 2 inches of the rim.

Throw a dart at a circular target.
Suppose you throw a dart at a circular target of radius 10 inches. Assuming that you hit the target and that the coordinates of the outcomes are chosen at random, find the probability that the dart falls
(a) within 2 inches of the center.
(b) within 2 inches of the rim.
(c) within the first quadrant of the target.
(d) within the first quadrant and within 2 inches of the rim.

Exponential Distribution for Radioactive Particles
Suppose you are watching a radioactive source that emits particles at a rate described by the exponential density
f(t) = λe−λt ,
where λ = 1, so that the probability P(0,T) that a particle will appear in
the next T seconds is P([0,T]) = T
0
λe−λtdt. Find the probability that a
particle (not necessarily the first) will appear
(a) within the next second.
(b) within the next 3 seconds.
(c) between 3 and 4 seconds from now.
(d) after 4 seconds from now

Light Bulb Failure and Reliability
Assume that a new light bulb will burn out after t hours, where t is chosen from [0,∞) with an exponential density f(t) = λe−λt .
In this context, λ is often called the failure rate of the bulb.
(a) Assume that λ = 0.01, and find the probability that the bulb will not burn out before T hours. This probability is often called the reliability of the bulb.
(b) For what T is the reliability of the bulb = 1/2?
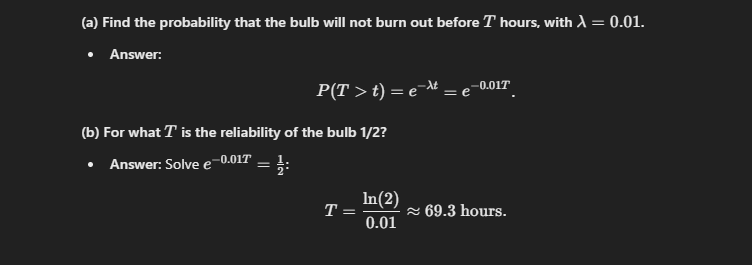





+ There are no comments
Add yours